Ill keep it short.
Since my last project, the smart-cloud-like-lamp, I wanted to learn how to use NTP synchronization.
Time synchronization issues came up quite often while I developed autonomous drones back in The MakersPlace, and (surprisingly) it's also come up here at Augury's IoT devices.
That's what I like to call a real-world problem :)
While I worked on the smart-cloud-like-lamp project, I stuck an RTC chip inside the main cloud:
An RTC chip has a battery and a crystal that ticks at a constant rate - as long as the battery has juice (Don't worry these things last around 10 years, give or take).
This RTC helps the main cloud keep track of the current time and date, so it could calculate the color relative to the time of day.
NTP synchronization
Another way that keeps track of time.
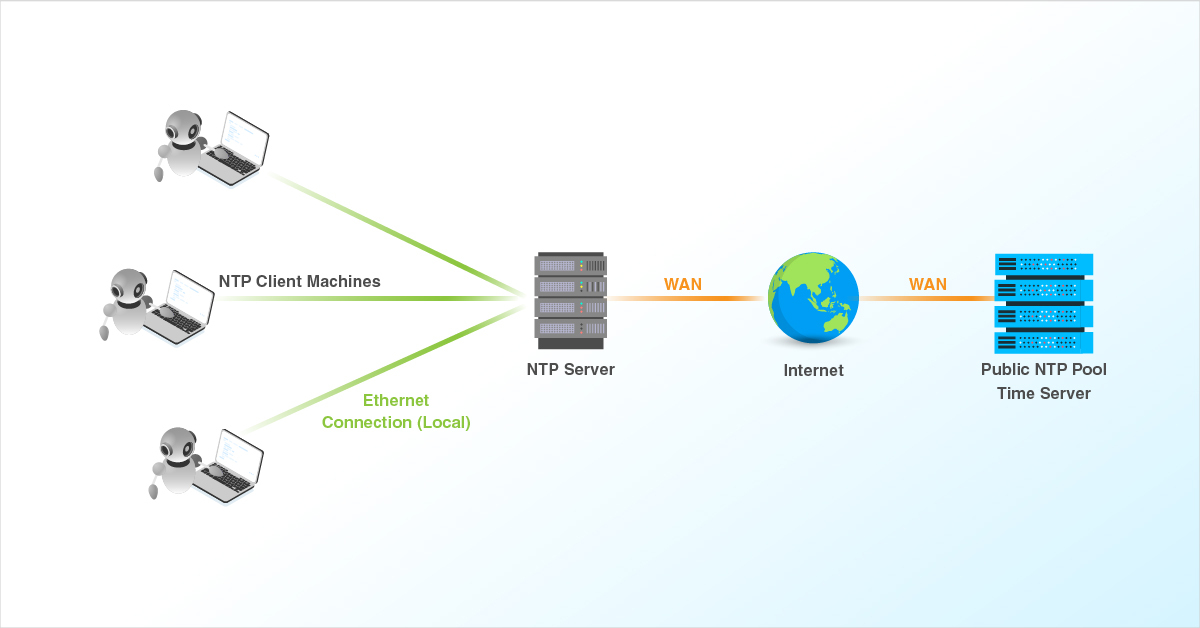Using NTP one must be connected to the internet.
Surprisingly, using NTP + Arduino is super easy
As easy as this one-liner:
const char *ntpServer = "pool.ntp.org";
const long gmtOffset_sec = 2 * 60 * 60;
const int daylightOffset_sec = 3600;
void setup()
{
//init and get the time
configTime(gmtOffset_sec, daylightOffset_sec, ntpServer); // ESP32 built in configurator
}
Basically, that's it
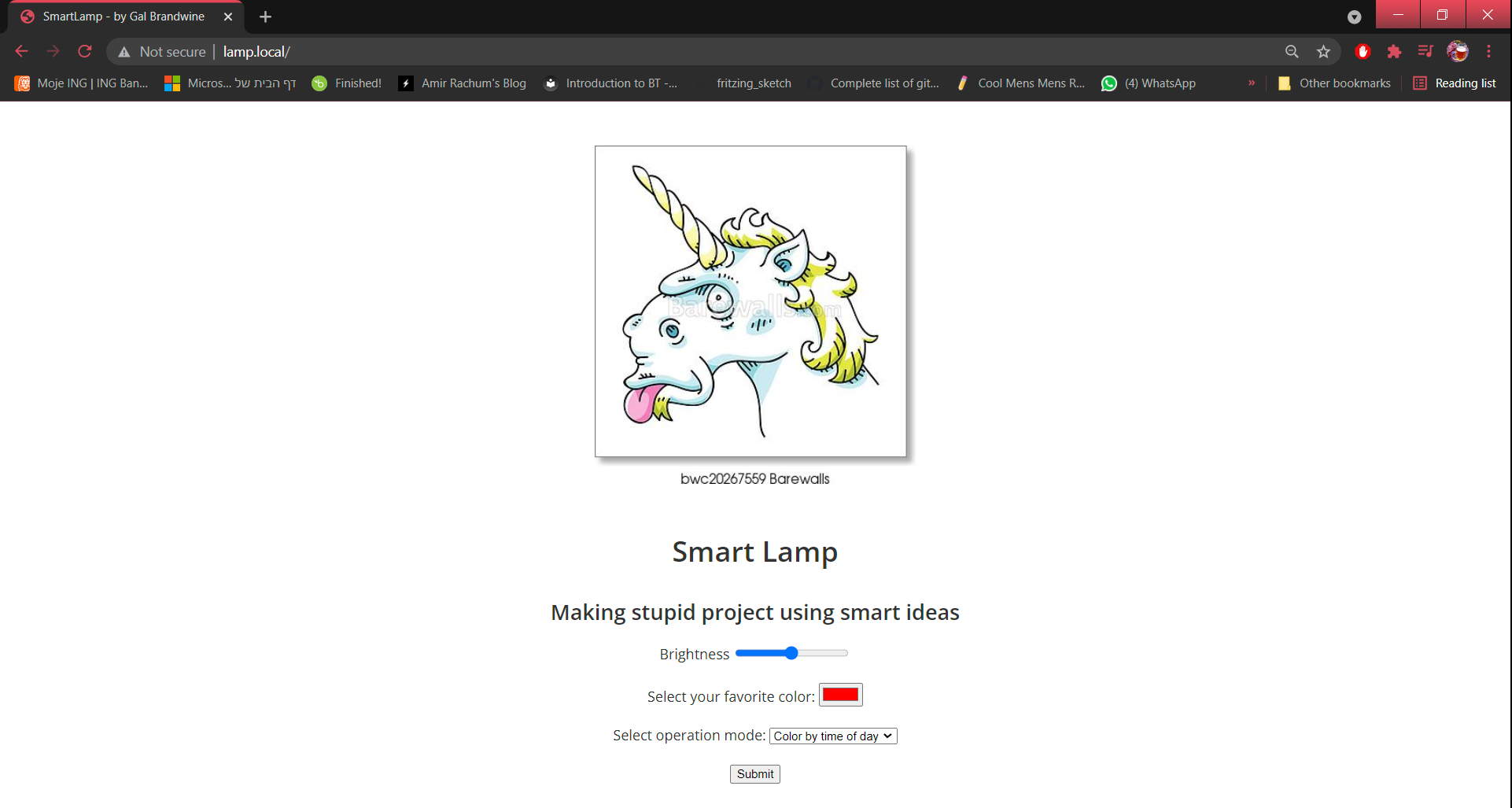
Project done, an NTP synchronized smart-lamp:
I've also thrown in some Mdns a simple landing page, and make use of the notorious WifiManager library.
But really - that's it.
Really!
The landing page:
Here's the GitHub repository - SimpleSmartLamp
It will be a shame to wrap it up there, there is so much more tweaking to be done
I always like to add some nerdy stuff :)
When I built the smart-cloud-like-lamp, I used a linear time to color mapping, much like this:
$x = \text{hour} \in [0,24]$
$y = \text{angle} \in HSV_{colorSpectrum}$
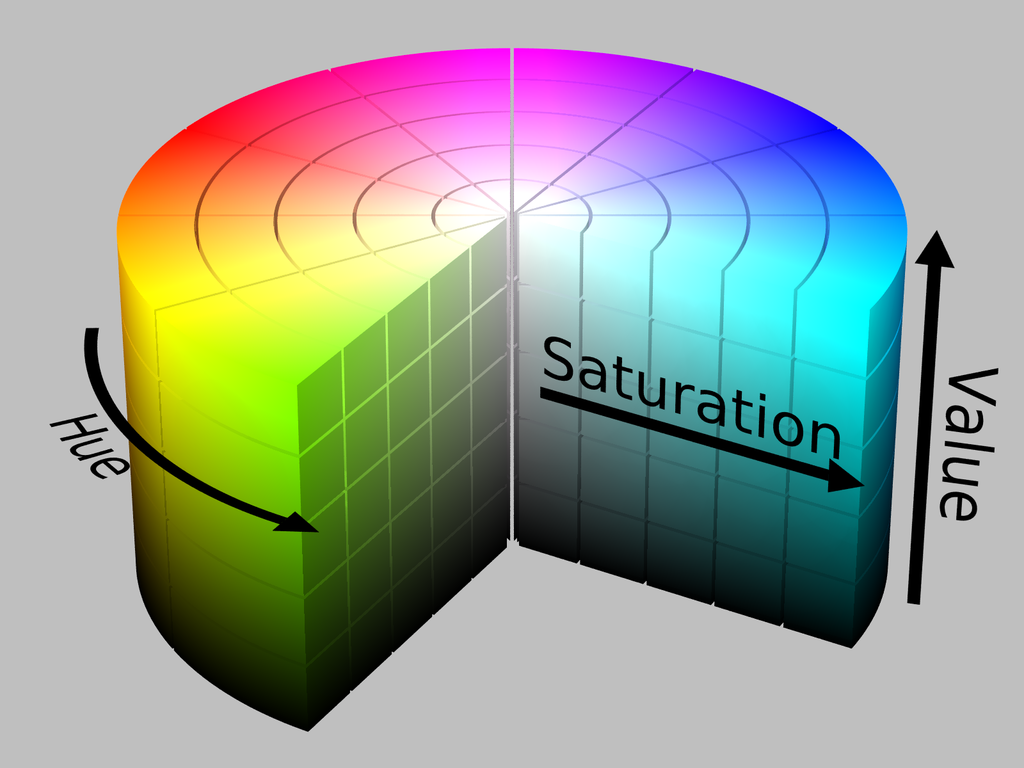
An HSV reminder:
$\theta=0 \rightarrow HUE_{val} \equiv \text{red color}$
$0<\theta<360 \rightarrow \text{we get all color spectrum}$
$\theta=360 \rightarrow HUE_{val} \equiv \text{red color}$
While the previously described hour-to-color linear mapping function works fine, this time I wanted to use a nonlinear mapping.
This is my nonlinear color mapping algorithm:
Which I'm very proud of :)
Step 1.
$map(hr) \rightarrow h_{mappedHour} \in [-1.0,1.0]$, where:
$$map(hr) = \frac{(\text{hr} - 0)*(1-(-1))}{(24-0)+(-1)} = h_{mappedHour}$$
One can see that when $x=11.5,y=1$ which is almost mid-day (out of 24 hrs). So it means my simple map function works, hip hip hooray!
Step 2.
Now we can use the gaussian curve function to find out the normalized $\text{HUE}_{normalized} \in [0,1.0]$:
$$\text{HUE}_{normalized} = (\frac{1}{\text{stddev}*\sqrt{2\pi}})e^{\frac{-1}{2}(\frac{h-\mu}{\text{stddev}})^2}$$
- $h$ is $h_{mappedHour}$
- $\text{stddev} = 0.4$ I used it only to fit the Gaussian curve to my color problem so that the peak of the curved will be at $y=1$
- $\mu = 0$ Mean value shifts the distribution on the $X$ ax, If it is 0 then it is centered around 0.
In the RED curve:
$x$ represents an hour of the day, where 12:00 is midday, hence mapped to 0. -12.5 is mapped to 00:00.
$y$ is the relative normalized hue value.
All I have left is to calculate back the real HUE value:
$$\text{HUE} = \text{HUE}_{normalized} * 360$$
And that's it, I have successfully calculated a HUE representing the time of day, in a nonlinear manner.
- In midday, $(x = 0, y = 360)$ - according to the HUE value, the color will be RED.
- The color will get colder as the time pass from 0 to 6 am, and from 12pm to 18 pm.
Final thoughts
I've never composed complex mathematical functions to accomplish simple ideas, it's a powerful tool, that I hope I'll keep using in my day-to-day challenges.
If I would like to readjust the HUE value I get, I can always shift, after all, HUE is cyclic. This is important to know if one wants that at midday the value will be blue and not red, for example.
Cheers, Gal